Potential Energy - Gravitational and Elastic. Concepts.

Potential Energy, Concepts
and Example.-

An object has energy when it is moving, but it can also have potential energy, which is the energy associated with the object's position.

Potential Energy, Example: a heavy brick lifted up has potential energy due to its position in relation to the ground. It can do work because when dropped it will fall because of the gravity force, allowing it to make a work output over another object receiving the impact.

A compressed spring has potential energy. For instance, the spring of a mechanical clock transforms its energy doing work to move the seconds, minutes and hour pointers.

There are several kinds of potential energy: gravitational, elastic, electric, etc.

Gravitational Potential Energy

The gravitational potential energy is a very common example of potential energy.

The Gravitational Potential Energy (GPE) of an object of mass m at a height y over a reference level is defined as:

EPG = mgy
g is the gravity acceleration

This definition is fully compatible with the definition of work since the work needed lo lift the mass m from the reference level to the height y is Fy = Weight·y = mgy. The object has gained an energy mgy.

If we let this object of mass m to fall freely by gravity on a stake on the ground, the work on the stake will be equal to the kinetic energy acquired while falling.

This kinetic energy can be calculated by the kinematics equation v_f² = v_i² + 2gy. Since v_i = 0, then
vf² = 2gy. The kinetic energy just before striking the stake is ½mv_f². Replacing v_f² with 2gy we get ½ m·2gy = mgy.

Then, to raise an object of mass m to a height y we need a work amount equal to mgy, and once at this height y, the object has the capability of doing work equal to mgy.

Let's notice GPE depends on the object's vertical height over some reference level; in this example, the ground.

The work needed to lift an object does not depend on the lifting path. That direction can be vertical, inclined, or another, and the work to rise the object will be equal.

Also, the work the object is able to do when falling does not depend on its path.

From what level must the height y be measured? What matters here is the potential energy change and we choose a reference level convenient to solve a given problem. Once we choose it, we must keep it during the calculations.

Elastic Potential Energy.

It is the energy associated with elastic materials. Next, we demonstrate the necessary work to compress or stretch a spring over a distance x is ½kx², where k is the spring's constant.

By Hook's Law, the relation between force and displacement on a spring is F = -kx. The minus sign is due to the force always pointing to the equilibrium position (x = 0). The force F is now variable and we can no longer use W = Fdcos.

Let's first find a general relation to calculate the work done by a variable force. We will apply it to our spring.

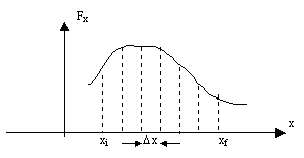
As F_x is nearly constant in each x, W F_x _x, the total work can be approximated by the formula

If we make the intervals x even shorter, this is, we make x 0, W tends to a limit, this can be expressed as

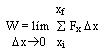
This formula represents the integral of the force Fx as a function of x:

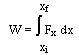
And this is the area under the curve F_x(x). Of course, this relation includes the case where F_x = F cos is constant.

Applying that relation to the spring, assuming the spring is placed horizontally and connected to a mass sliding over a smooth surface which is also horizontal, and that the spring is compressed over a distance x_max and then released, the work W done by the spring force between x_i = -x_max and x_f = 0 is:

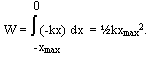
Physics Homework, Site Links

· Energy, Work and Power: Concepts
· Kinetic Energy
· Potential Energy
· Power