Examples Of Physics Homework Help: Solved Mechanical Energy Conservation Problems

Solved Physics Homework Problems on Mechanical Energy Conservation.

Our physics homework helper will send you his online answers to your physics homework in a similar way as shown with the problem examples shown below. All online help is sent as attachments by email and also by fax upon request.

Example One, Homework Help, Problem Solution: Conservation of Energy Applied to a Case of a Spring Compression.

A ball of mass m is placed at a distance h above the end of a vertical spring. The ball is then released and compresses the spring. The elastic constant of the spring is k. What is the maximum spring deformation? Assume no friction.

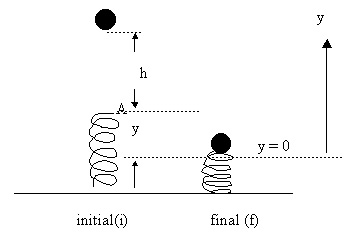
The image above shows the initial and final situations for this problem.

It is convenient to choose the lowest point reached by the ball as the reference level (y = 0) . We could choose a point such as point A, but it would have the disadvantage of having to deal with positive and negative potential energies.

Let's notice that in the final situation the ball is momentarily stop and its kinetic energy becomes zero at the stop point.

The following table help us to explain the solutions steps:

Initial situation Final situation

Kinetic Energy Ec_i = 0 Ec_f = 0

Gravitacional Potential Energy Epg_i = mg(h + y) Epg_f = 0

Elastic Potential Energy Epe_i = 0 Epe_f = ½ ky².

Then, as the initial energy must equal the final energy,

(Ec + Epg + Epe)_i = (Ec + Epg + Epe)_f, we obtain:

mg(h + y) = ½ ky².

The maximum deformation or compression of the spring is obtained solving for y in this quadratic equation. The parameters m, h and k are the known data.

For example, suppose a ball of mass m = 0,4 kg is dropped from a height h = 1.2 m and an the elastic constant k = 100 N/m. Replacing this data and solving the equation we get y = 0.35 m or 35 cm.

Example Two, Homework Help, Problem Solution: Conservation Of Energy Applied to a Vehicle Braking Within a Distance.

An automobile travels with a speed of 72 km/h. Assume that when the brakes are fully pressed, it can be stopped on a 25 meters distance. If the vehicle had double velocity, 144 km/h, what will its braking distance be?. Let's also assume that the friction force between tires and ground is nearly constant. Also calculate the coefficient of friction.

Solution:

We can use "work done on an object is equal to its kinetic energy change" , W = Change in Ek = Ek = Ekf - Eki. W is the net work done on the object. As the force is supposed to be constant, the work done by the friction force F is Fd, where d is the braking distance. F and d are in opposite directions, so W is negative. The final velocity is zero. Then

W = - Fd = Ek = 0 - ½ mv².

d = ½ mv²/F.

m and F are constants, so it is clear that the braking distance increases proportionally with the square of velocity.

The braking distance for the 144 km/h velocity is 100 meters, four times the braking distance needed for 72 km/h.

To calculate the coefficient of friction, we use Fd = ½ mv².

F= µmg, µ is the friction coefficient and m is the vehicle mass.

µmgd = ½ mv².

The velocity is 72 km/h = 72/3.6 m/s = 20 m/s and d is 25 m.

Then µ = ½ v²/gd = ½ (20 m/s)²/(9.8 m/s² 25 m) = 0.816 .

Note: You can see more about our physics homework help by pressing the link below that says "Physics, Detailed Homework Scope Help".

Sites With Solved Exercises on Mechanical Energy

· Physics Homework - Examples of Mechanical Energy Problems