Electric Field,
A Useful Definition.

The electric field is a concept similar to the gravitational field. In both, there exists a force acting from some distance. This was not easy to accept for the ancient scientists.

The electric field idea was developed by Michael Faraday. For him an electric field spreads outward from every charge invading all the space. When a second charge is located near the first one, it "feels" a force due to the electric field already present. That is, the electric field in the place of the second charge interacts directly with that charge to produce the force.

You can measure the electric field surrounding a charge, a group of charges or a continuous distribution of charges, by measuring the force on a small positive test charge. The test charge must be understood as a very small positive charge not altering the rest of charges distribution making up for the field to measure.

To make it more clear, assume a unique positive charge Q. We want to measure its field through placing a test charge q (positive and small) in the points a, b and c.

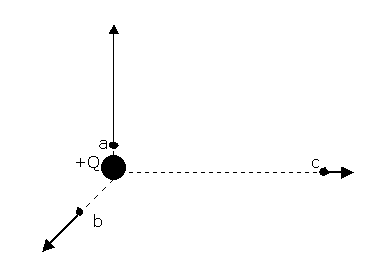
We know the forces are radially directed out of Q and that its magnitudes are given by Coulomb's Law. The electric field in the points a, b and c is defined in terms of the force over that test charge.

The electric field E, in any point of the space is defined as the force F exerted over a test charge in that point, divided between the magnitude q of the test charge:
E = F / q

Let's notice this definition is similar to that of a gravitational field where g is the gravitational field and F_g is the gravitational force acting on a test mass m, g = F _g/ m.

With this definition, the direction of the electric field at any point in the space is defined as the direction of the force over a positive test charge placed in that point. The magnitude of the electric field is the force per unit charge, so E is measured in Newton/Coulomb (N / C).

Any electric field can be measured using the above definition, whether dealing with a point charge or distributed charges. A simple case is to calculate E at a distance r from a unique point charge Q. As the magnitude of the force on the test charge is
F = (k q Q)/r², is easy to demonstrate that the electric field is

E = F / q = k Q / r².

Notice the electric field is independent of q, the test charge.

Electric Field Exercise.

Let's do an exercise for a better understanding this: Calculate the magnitude and direction of the electric field on a point P placed 20 cm to the right of a point charge Q = - 2.0 x 10^-6 C.

Solution:
The magnitude of the electric field is:
E = k Q / r² = (9 x 10⁹ N m² / C²)(2.0 x 10^{- 6}C)/(0.2 m)² = 450 x 10³ N / C. The direction of the electric field is towards the charge Q, because Q is negative and the test charge is always positive.

Note: For a full scope of our homework physics help, you can press our link for related sites named "Physics, Detailed Homework Scope Help".

More Electric Field Exercises, Press Here

Electric Field, A Useful Definition.

Electric Field Exercise.

Electric Field,
A Useful Definition.