Sum of Vectors. Problems Dealing With Relative Velocity

Application Problems: Use of Addition Vector Tools to Solve Relative Velocity

Vector Problems, Example One.-
A motorboat velocity is 20 km/h in still water. If the boat must travel straight to the nearest shore in a river whose current is 12 km/h, ¿What up stream angle must the bow boat point at?

Before attempting to solve this problem, it is useful to do some considerations:
- Whenever a velocity is mentioned, it is necessary to specify what is its frame of reference to measure it. This is a case where we have relative velocities and the tool to find the resultant or the components is the vector sum.
- It is helpful to use an identification procedure that uses two sub indexes: the first sub index refers to the object and the second one to the frame of reference in which that velocity is measured. In this example V_BW is the velocity of the Boat relative to the Water, V_BS is the Boat velocity relative to the Shore and V_WS is the Water velocity relative to the Shore. Notice V_BW is produced by the boat motor, instead V_BS is V_BW plus the current effect. Hence, the boat velocity relative to the shore V_BS, is

(A) V_BS = V_BW + V_WS

The sentence "a motorboat velocity is 20 km/h in still water" means V_BW = 20 km/h, and the sentence "a river whose current is 12 km/h" means V_WS = 12 km/h. Notice V_BS points directly straight to the opposite shore as wanted. The angle can be obtained from the rectangular triangle in the figure:
sen = V_WS/V_BW = 12/20 = 0.6 then = 36.87º. The bow boat must point at an angle of 36.87º up stream in order to cross the river directly to the other shore.

Vector Problems, Example 2.-
A boat velocity is 2 m/s in still water. a) If the boat points the bow straight to the opposite shore to cross the river whose current is 1 m/s, what is the velocity, in magnitude and direction, of the boat relative to the shore? b) What is the boat position relative to its starting point, after 3 min?

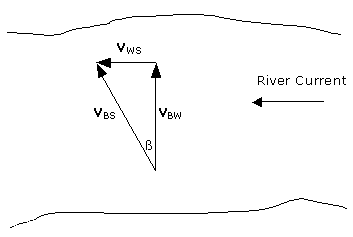
a) The boat velocity relative to the shore V_BS, is the sum of its velocity relative to the water V_BW, and the water velocity relative to the shore V_WS :

V_BS = V_BW + V_WS

As V_BW and V_WS are the sides of a rectangular triangle,
V_BS² = V_BW² + V_WS² or
V_BS² = (2m/s)² + (1m/s)² i.e. V_BS = 2.24 m/s.
Also, tan = V_WS/V_BW = 1/2 , then = 26.57º.

b) To calculate the position after 3 min we can use D = Vt, with D the vector displacement, V the vector velocity and t the time, an scalar. The direction of D is the same as V and its magnitude is V·t = 2.24 m/s·3·60 s = 403.2 m. The boat position is then at 403.2 m from the starting point and at a direction 26.57º down stream transverse to it

Vectors, Related Sites, visit:
· Vectors, Scalars
· Vectors, Scalars - Analytic Method