Exercises Using Ohm’s Law

Homework Exercises, Ohm's Law,
Example One
The circuit below is called a Wheatstone bridge. It is used for measuring resistance. Show that when the current through the galvanometer G is zero, then R₁ = R₂(R₃/R₄). Thus, if we know R2 and the ratio (R₃/R₄), we can obtain the resistance R₁.

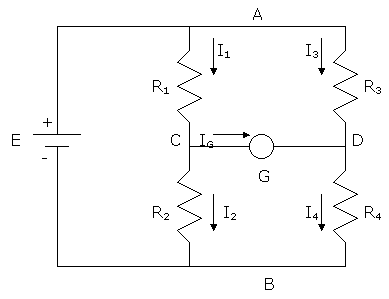
I_G = 0 means points C and D are at the same potential and
that I₁ = I₂, I₃ = I₄.

By Ohm’s law V_AC = I₁R₁, V_AD = I₃R₃, V_CB = I₂R₂, V_DB = I₄R₄.

As V_AC = V_AD and V_CB = V_DB, then I₁R₁= I₃R₃,
I₂R₂= I₄R₄.

As I₁ = I₂ and I₃ = I₄, then doing I₁R₁/ I₂R₂=I₃R₃/I₄R₄ we get R₁= R₂(R₃/R₄).

Homework Exercises, Ohm's Law,
Example Two
Determine the total resistance and potential difference between points a and b in the circuit shown. Also determine the current in, and the potential difference across, each resistor. The input current is 60 A.

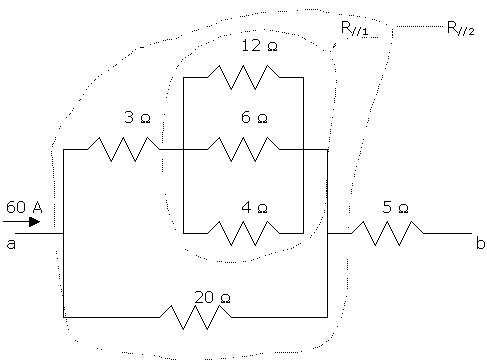
a) Total resistance between a and b.

First, calculate the 12, 6, and 4 ohm parallel combination R_//1
1/R_//1 = 1/12 + 1/6 + 1/4 = 1/2. Then R_//1 = 2 ohm.

The upper branch is 3 ohms in series with R//1, 3 ohm + 2 ohm = 5 ohm.

This 5 ohm resistor is in parallel with the 20 ohm resistor, equivalent to a single resistor R_//2 = 5 ohm//20 ohm:
1/R_//2 = 1/5 + 1/20 = ¼. Then R_//2 = 4.
The total resistance between a and b is 4 ohm + 5 ohm = 9 ohms. The voltage drop or potential difference between points a and b is 60Ax9ohm = 540 V.

b) To obtain the individual currents and voltages in each resistor we can proceed as follows (there is no a unique method):

The voltage across R_//2 is the difference between the total 540 voltage and the voltage drop in the 5 ohm resistor. This drop is 60Ax5ohm = 300 V. So the potential difference across R_//2 is 540 V – 300 V = 240 V.
Now we can calculate the currents and voltages in the R_//2 combination:
In the 20 ohm resistor: current= 240 V/20 ohm = 12 A, voltage = 240 V
The upper branch has then a current of 60 A - 12 A = 48 A, or alternatively 240 V/5 ohm = 48A.
The 3 ohm resistor has a voltage of 48 Ax3 ohm = 144 V.
The R_//1 combination presents a voltage of 48 AxR_//1 = 48 Ax2 ohm = 96 V, or alternatively 240 V - 144 V = 96 V.
The currents in the 12 ohm, 6 ohm and 4 ohm are respectively 96/12 A=8 A, 96/6=16 A and 96/4=24 A.

Homework Exercises, Ohm's Law,
Example Three
Given the resistor arrangement shown below, prove that the relation between R₁ and R₂ must be R₂=1.618R1 in order that the resistance of the system R be equal to R₂.

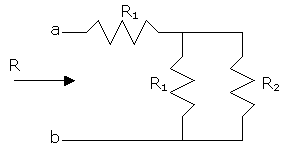
R=R₁+R₁//R₂=R₁+R₁R₂/(R₁+R₂).
The condition is R=R₂, so we do
R₂=R₁+R₁R₂/(R₁+R₂).
R₁R₂+R₂²=R₁²+R₁R₂+R₁R₂.
0= R₂² - R₁R₂ - R₁².

This is a second degree equation in R₂, whose solution is R₂= R₁(1/2 ± )

Disregarding the minus sign we get R₂ = 1.618R₁.

Ohm's Law Principle