Second Newton's Law Exercise. Free Body Diagram

Second Newton's Law Exercises

Inclined Plane, Detailed Example With and Without Friction

The pulley shown below is weightless and frictionless. The block of mass m₁is on the plane, inclined at an angle with the horizontal. The block of mass m₂ is connected to m₁ by a string.

a) Assuming there is no friction, show a formula for the acceleration of the system in terms of m₁, m₂, and g.
b) What condition is required for m₁ to go up the incline?
c) Assume that the coefficient of kinetic friction between m₁ and the plane is 0.2, m₁ = 2 kg, m₂ = 2.5 kg and the angle = 30º. Calculate the acceleration of m₁ and m₂.
d) What is the maximum value of the friction coefficient so the system can still move.

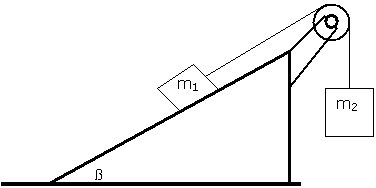
Before attempting to solve a Second Newton's Law problem like this it is very useful to take into account the following considerations:

Free Body Diagram.- In every problem where the Second Newton's Law applies it is fundamental to draw what is called the Free Body Diagram. This diagram must show all the external forces acting on a body. We isolate the body and the forces due to that strings and surfaces are replaced by arrows; of course, the friction forces and the force of gravity must be included. If there are several bodies, a separate diagram should be drawn for each one.

FREE BODY DIAGRAM

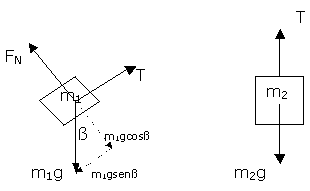
- The force that m₁ exerts on m₂ through the rope has the same magnitude T. This is so because a rope only changes the direction of a force, not its magnitude assuming a weightless rope.

- The magnitude of the acceleration is the same at both ends of the rope assuming an inextensible rope.

Components of Force.- Notice from the diagram the weight of m₁ has been split into the components m₁gsen parallel to the incline, and m₁gcos perpendicular to it.

a) Let's assume the direction of the acceleration makes m₁ to go upward.
Sum of forces on m₁ in the direction of the incline: T-m₁gsen=m₁a
Sum of vertical forces on m₂ = m₂g-T = m₂a
And adding both equations we get m₂g-m₁gsen = a(m₁+m₂)
Or a = g(m₂-m₁senß)/(m₁+m₂)

b) For a to be positive (i.e. m₁ going up) m₂ > m₁sen
For a to be negative(i.e. m₁ going down) m₂ < m₁sen

c) Now appears a friction force, always in an opposite direction to the movement. The magnitude of this friction force is F_f = F_N. F_N is obtained using:
Sum of forces perpendicular to the incline = F_N-m₁gcos = 0
or F_N = m₁gcos. The friction force is then F_f = m₁gcos
The sum of forces on m₁ in the sense of the incline is now
(1) T-m₁gsen-m₁gcos = m₁a
The sum of vertical forces on m₂ is
(2) m₂g-T = m₂a

Adding (1) and (2) we get m₂g-m₁g(sen+µcos) = a(m₁+m₂)
Replacing values, with = 0.2, m₁ = 2 kg, m₂ = 2.5 kg and = 30º results a = 2.51 m/s².

d) As the coefficient of friction increases, the acceleration decreases until reaching a value near zero or zero. This condition is obtained with zeros in the right side of equations (1) and (2) used before in answer c):
T-m₁gsen-m₁gcos = 0
m₂g-T = 0
And adding, we get m₂g-m₁gsen-m₁gcos = 0
Or = (m₂-m₁sen)/m₁cos
Replacing values we get = 0.87.

Newton's Second Law Links:
Second Newton's Law, Theory and Examples
Second Newton's Law Examples, Part One