Gauss' Law Exercises, Problem One
Using Gauss' Law, obtain the electric field created by a charge uniformly distributed over a plane.
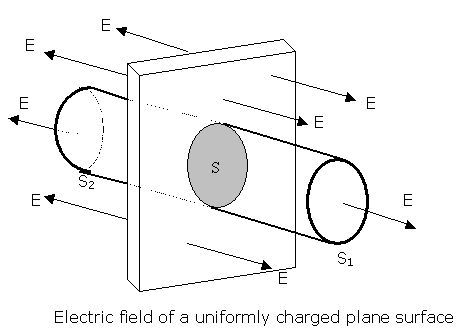
Solution.- The figure represents a plane which carries a positive charge a per unit area. The electric field is perpendicular to the plane due to the symmetry of the problem. Choosing for our closed surface the cylinder shown in the figure, we may separate the electric flux Ø into three terms: The flux through S1 which is +ES, where S is the area of the base of the cylinder ; the flux through S2, which is also +ES, and the flux through the lateral surface of the cylinder, which is zero because the electric field is parallel to the surface. Therefore we have Ø = 2ES. The charge inside the closed surface is that in the shaded area and is equal to q = aS. Applying Gauss' Law we have
![]()
Gauss' Law Exercises, Problem Two
A solid conductor sphere of radius a has a positive net charge 2Q. A conductor spherical shell of inner radius b and external radius c has the same center with the solid sphere and has a net charge -Q. Using Gauss' Law determine the electric field in the regions denoted as (1), (2), (3) y (4) in the figure below, and the charge distribution over the shell when all the system is in electrostatic equilibrium.
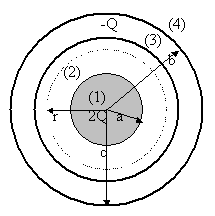
Solution.- To find E in the inside of the solid sphere, region (1), consider a gauss' surface of radius r < a. Since there is no charge inside a conductor in electrostatic equilibrium, it is clear that qin = 0. Then, based on Gauss' Law and the symmetry, E1 = 0 for r < a.
In the region (2) - between the solid sphere surface and the inner shell surface - consider a spherical gauss' surface of radius r where a < r < b. The charge inside this surface is +2Q (the charge on the solid sphere). Due to the spherical symmetry the electric field lines must point with its radius outward and have constant magnitude over the Gauss' surface. Using Gauss' Law it is found that
![]()
In the region (4), where r > c, the spherical Gauss' surface encloses a total charge qin = 2Q - Q = Q. Then, Gauss' Law applied to this surface produces
![]()
In the region (3) the electric field must
be zero due the spherical shell is also a conductor in equilibrium. As E3
= 0, the Gauss Law applied to the surface with radius r where b < r < c implies
qin = 0. Therefore the charge over the inner
spherical shell surface must be -2Q to cancel the + 2Q charge on the solid
sphere. As the net charge on the shell is - Q, it is concluded that the external
shell surface must have a +Q charge.
Other Physics Sites:
· Physics, Main Page
· Physics, Mathematics
· Physics, Detailed Homework Scope Help
· Energy, Work and Power: Concepts
· Kinetic Energy
· Potential Energy
· Power
· Physics Problems, Example
· Physics Homework - Mechanical Energy Conservation Problems
· Physics Homework - Mechanical Power Problems
· Coulomb's Law
· Exercises Using Coulomb's Law
· Electric Field Charges
· Electric Field Exercises
· Electric Potential Energy
· Exercises, Electric Potential Energy
· Ohm's Law, Principle
· Ohm's Law Exercises
· Second Newton's Law
· Second Newton's Law Examples, Part One
· Second Newton's Law Examples, Part Two
· Sound Waves
· Sound Waves: Standing, Interference, Doppler Effect - Examples
· Sound Waves, Doppler Effect - Examples
· Vectors, Scalars
· Vectors, Scalars - Analytic Method
· Addition Vector Tools, Problems
· Free Fall Theory
· Free Fall Exercises, Part One
· Free Fall Exercises, Part Two
· Free Fall Exercises, Part Three