Physics: Vectors, Scalars. Graphic and Analytic Sum

VECTORS AND SCALARS

In physics we must distinguish between vector quantities and scalar quantities.

A vector is an oriented quantity, it has magnitude and direction like velocity, force and displacement.

Scalars have no direction associated to them, only magnitude, like time, temperature, mass and energy.

Vectors are represented by arrows where the length of the arrow is drawn proportionally to the magnitude of the vector.

The letters denoting vectors are written in boldface.

1.- VECTORS ADDITION. GRAPHIC METHOD.

To add scalars like mass or time, ordinary arithmetic is used.

If two vectors are in the same line we can also use arithmetic, but not if they are not in the same line. Assume for example you walk 4 km to the East and then 3 km to the North, the resultant or net displacement respect to the start point will have a magnitude of 5 km and an angle = 36.87º with the positive x direction. See figure.

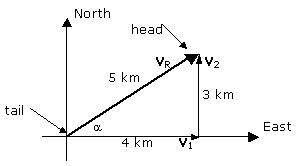
The resultant displacement V_R , is the sum of vectors V₁ and V₂, that is we write

V_R = V₁ + V₂ This is a vector equation.

The general rule to sum vectors in a graphic way (geometrically) which is in fact the definition how vectors are added, is the following:

(1) Use a same scale for the magnitudes.
(2) Draw one of the vectors, say V₁.
(3) Draw the other vector V₂, placing its tail on the head of the first one, making sure to keep its direction.
(4) The sum or resultant of the vectors is the arrow drawn from the tail of the first vector to the head of the second vector.

This method is called vector addition from tail to head.

Notice that V₁ + V₂ = V₂ + V₁, that is, the order does not matter.

This tail to head method can be extended to three or more vectors. Suppose we want to add the vectors V₁, V₂ and V₃ shown below:

V_R = V₁ + V₃ +V₃ is the resultant vector outlined with a heavy line.

A second method to add two vectors is the parallelogram rule equivalent to the tail to head method. In using this parallelogram rule the two vectors are drawn from a common origin and a parallelogram is formed using the two vectors as adjacent sides. The resultant is the diagonal drawn from the common origin.

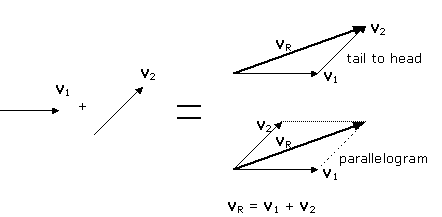
2.- SUBTRACTION OF VECTORS

Given a vector V it is defined the negative of this vector (-V) as a vector with the same magnitude as V but opposite direction:

The difference of two vectors A and B is defined as per this equation:

A - B = A + (-B)

So we can use the addition rules to subtract vectors.

3.- MULTIPLICATION OF A VECTOR BY A
REAL NUMBER.

A vector V can be multiplied by a real number c. This product is defined in such a way that cV has the same direction as V and magnitude cV. If c is positive, the sense is not altered. If c is negative, the sense is exactly opposite to V.

More on This Theme:
· Vectors, Scalars - Sum: Analytic Method
· Vectors, Addition Tools, Problems