1) S : Sample space or set of all the
possible results.
2) A
B : al least
one of the events A or B occurs.
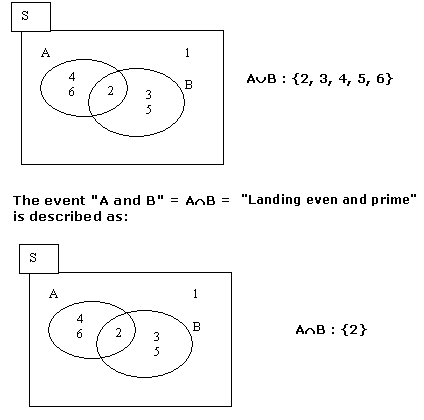
3) A
B : both
events occur.
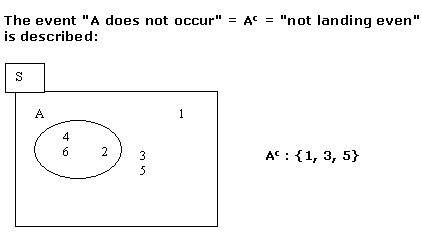
4) Ac : The event A does not occur.
Example:
In the experiment "tossing a die of six sides" let the events:
A = landing even, B = landing prime.
The event "A or B" = AB
: "landing even or prime" is described as:
If S is a set of n elements and A is
a subset of k elements, then
P(A) = k/n, according with the definition of probability.
Properties
Besides
P(S) = 1, P(
) =
0, 0 
P(A)
1, we have:
1) If AB =
(A and B are mutually exclusive) then:
P(AB)
= P(A) + P(B)
2)P(A)
+ P(Ac) = 1
3) If AB
then
P(AB)
= P(A) + P(B) - P(AB)
4) If A and B are independent events
( the occurence of A do not
affect
the occurrence of B), then
P(AB)
= P(A)·P(B)
5) If A and B are dependent events
(the occurrence of A affects the occurrence
of B), then
P(AB)
= P(A)·P(B/A)
P(B/A) is the
probability of B, knowing that A has occurred.
Examples of Probability Properties
1) P(AB)
= P(A) + P(B). A card is drawn from a standard deck of 52 cards. Assume we
define the events A: "landing 3" and B: "landing a figure" and we are asked
for the probability of A or B. As these events cannot occur simultaneously,
P(A or B) = P(AB)
= P(A) + P(B) = P(drawing 3) + P(drawing figure) = 4/52 + 12/52 = 4/13.
2) P(A) + P(Ac) = 1. In
the same last experiment, the event A: "not drawing King " has as complement
the event "drawing King", then it is more simple to calculate the probability
of A as 1 - P(Ac):
P(not drawing
King) = 1 - P(drawing King) = 1 - 4/52 = 12/13
3) P(AB)
= P(A) + P(B) - P(AB).
When tossing a six-sides die, the events A: "landing even" and B: "landing
prime", have no empty intersection: AB
= {2}, the probability of the event "landing even or prime" = A or B is
P(A or B)=P(AB))=P(A)+P(B)-P(AB)=3/6+3/6-1/6=5/6
4) P(AB)
= P(A)·P(B). A six-sided die is tossed two times. The events A: "landing even
in the first tossing " and B: "landing a 3 in the second tossing", are independent
events, then the probability of "landing even in the first trial and a 3 in
the second trial" is
P(A y B) = P(AB)
= P(A)·P(B) = (3/6)·(1/6) = 1/12
5) P(AB)
= P(A)·P(B/A) or P(B/A) = P(AB)/
P(A) [P(B/A) is the probability of event B, knowing that A has occurred. In
drawing a card from a standard deck of 52 cards, what is the probability that
the drawn card be the ace of hearts, knowing that the drawn card is hearts
suit?
What is asked is P(ace/hearts). The probability "ace and hearts" is 1/52.
The probability of hearts is 13/52. Then, P(ace/hearts) = P(ace and hearts)/P(hearts)
= (1/52)/(13/52) = 1/13.
Probability Definitions
Mathematics, Help Scope